Sebelum memilih jenis dan sifat akar dari suatu persamaan kuadrat, pertama-tama tentu kita harus mengerti bagaimana bentuk persamaan kuadrat itu. Persamaan kuadrat biasanya dituliskan menyerupai pada kotak di bawah ini.
Pada persamaan tersebut dituliskan syarat bahwa a dihentikan sama dengan 0 alasannya yakni bila a = 0, maka persamaan itu akan menjadi persamaan garis lurus dimana b berfungsi sebagai gradien atau sering dilambangkan dengan m.
Jenis akar persamaan kuadrat bergantung pada nilai diskriminannya. Oleh alasannya yakni itu jenis-jenis akar suatu persamaan kuadrat ditentukan oleh nilai konstanta a, b, dan c dalam persamaan tersebut.
Pada persamaan tersebut dituliskan syarat bahwa a dihentikan sama dengan 0 alasannya yakni bila a = 0, maka persamaan itu akan menjadi persamaan garis lurus dimana b berfungsi sebagai gradien atau sering dilambangkan dengan m.
Jenis akar persamaan kuadrat bergantung pada nilai diskriminannya. Oleh alasannya yakni itu jenis-jenis akar suatu persamaan kuadrat ditentukan oleh nilai konstanta a, b, dan c dalam persamaan tersebut.
ax2 + bx + c = 0
melaluiataubersamaini :
a = koefisien dari x2
b = koefisien dari x
c = tetapan
Jenis-jenis Akar
Untuk mengetahui jenis-jenis akar dari suatu persamaan kuadrat sanggup dipakai persamaan diberikut :
D = b2 - 4ac
melaluiataubersamaini :
D = diskriminan
a = koefisien dari x2
b = koefisien dari x
c = tetapan
Jika nilai D sanggup dihitung, maka dengan simpel sanggup ditentukan jenis-jenis akarnya. Secara garis besar ada 3 jenis akar yang mungkin diperoleh dari suatu persamaan kuadrat, yaitu :
1. Akar real (D ≥ 0)
a. Akar real berlainan bila D > 0
misal : Tentukan jenis akar dari persamaan x2 + 4x + 2 = 0.
Penyelesaian :
Dari hasil perhitungan diketahui D > 0 maka akarnya ialah akar real tapi tidak sama.
b. Akar real sama, x1 = x2 bila D = 0Penyelesaian :
2. Akar tidak real/imajiner (D < 0)
misal : Tentukan jenis akar dari persamaan x2 + 2x + 4 = 0
Penyelesaian :
Dari perhitungan diperoleh D < 0 maka akar-akarnya yakni tidak real.
3. Akar rasional (D = k2)
misal : Tentukan jenis akar dari persamaan x2 + 4x + 3 = 0
Penyelesaian :
Karena D = k2 = 4 , maka akar persamaannya yakni akar rasional.
Sifat Akar
Sifat yang dimaksud dalam akar persamaan kuadrat yakni akar positif, negatif, tidak sama tanda, berlawanan, atau berkebalikan. Untuk melihat sifat akar, selain mencari nilai D, kita juga harus mencari hasil penjumlahan dan hasil perkalian akar-akar suatu persamaan kuadrat. Adapun rumus yang diapaki untuk memilih sifat akar yakni sebagai diberikut :
Sifat akar dari suatu persamaan kuadrat antaralain :
1. Dua akar aktual (x1 > 0 dan x2 > 0)
Akar-akar persamaan kuadrat dikatakan aktual bila :
- D ≥ 0
- x1 + x2 > 0
- x1 . x2 > 0
2. Dua akar negatif (x1 < 0 dan x2 < 0)
Akar-akar persamaan kuadrat dikatakan negatif bila :
- D ≥ 0
- x1 + x2 < 0
- x1 . x2 > 0
3. Dua akar tidak sama tanda (salah satu akar negatif)
Persamaan kuadrat mempunyai akar yang tidak sama tanda yaitu salah satu akar bertanda aktual dan yang lain negatif apabila perkalian kedua akarnya bernilai negatif (x1 . x2 < 0)
4. Sama besar berlawanan tanda (x1 = -x2)
Bila suatu persamaan kuadrat mempunyai nilai b = 0 atau berbentuk ax2 + c = 0, maka akar-akarnya akan mamiliki nilai yang sama dan berlawanan tanda.
5. Akar berkebalikan ( x1 = 1/x2)
Akar x1 akan berupa kebalikan dari akar x2 bila dalam suatu persamaan kuadrat nilai c dan a sama (a = c)










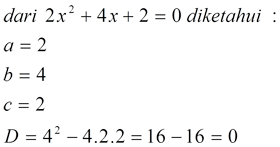



Emoticon