Pembahasan Un Fisika Perihal Momen Gaya Dan Inersia

.com - Momen Gaya (Torsi) dan Momen Inersia. Dalam belahan dinamika gerak rotasi, momen gaya dan momen inersia ialah dua subtopik yang paling umum dipelajari. Kedua bemasukan tersebut saling berhubungan. Momen gaya menyatakan besar gaya yang menjadikan benda berotasi sedangkan momen inersia menyatakan ukuran kelembaman suatu benda untuk gerak rotasi. Dalam soal ujian nasional bidang study fisika biasanya ada satu atau lebih soal yang berafiliasi dengan momen gaya atau momen inersia. Pada peluang ini, edutafsi akan membagikan pembahasan beberapa soal ujian nasional fisika ihwal momen gaya dan momen inersia sebagai citra untuk ujian nasional fisika diberikutnya.

Soal 1 : Menentukan Momen Gaya pada Bola

Sebuah bola pejal yang diameternya 20 cm berotasi dengan poros yang melalui sentra bola. Bola mempunyai persamaan kecepatan sudut ω = (10 + 25t) rad/s, dengan t dalam sekon. Jika massa bola 4 kg, maka momen gaya yang bekerja pada bola tersebut ialah ....
A. 0,32 Nm
B. 0,40 Nm
C. 0,65 Nm
D. 0,80 Nm
E. 1,60 Nm

Pembahasan :
Dik : d = 20 cm, R = 10 cm, ω = (10 + 25t) rad/s, m = 4 kg
Dit : τ = .... ?

Pada soal disebutkan persamaan kecepatan sudut benda. Secara umum, persamaan kecepatan sudut sanggup ditetapkan sebagai diberikut:
⇒ ω = (ω_o + α.t)

melaluiataubersamaini ω menyatakan kecepatan sudut benda sehabis t detik, ω_o menyatakan kecepatan sudut mula-mula, α menyatakan percepatan sudut, dan t menyatakan waktu. Berdasarkan persamaan tersebut, maka sanggup kita lihat nilai percepatan sudutnya:
⇒ ω = (10 + 25t) = (ω_o + α.t)

melaluiataubersamaini memakai konsep kesamaan, maka besar percepatan sudutnya ialah 25 rad/s². melaluiataubersamaini demikian besar momen gaya yang bekerja pada bola adalah:
⇒ τ = I . α
⇒ τ = 2/5 m.R² . α
⇒ τ = 2/5 (4) . (0,1)² . (25)
⇒ τ = 0,4 Nm

Jadi, momen gaya yang bekerja pada bola tersebut ialah 0,4 Nm.

Jawaban : B

Soal 2 : Menentukan Percepatan Tangensial Katrol

Sebuah katrol dari benda pejal dengan tali yang dililitkan pada sisi luarnya ditampilkan menyerupai gambar di bawah ini:

Gesekan katrol dengan tali dan ukiran di sumbu putarnya diabaikan. Jika momen inersia katrol I = β, dan tali ditarik dengan gaya tetap F, maka kekerabatan yang sempurna untuk menyatakan percepatan tangensial katrol ialah ....
A. α = F . R . β
B. α = F . R . β²
C. α = F . (R . β)^-1
D. α = F . R (β)^-1
E. α = (F . R)^-1 . β

Pembahasan :
Dik : I = β, F = F
Dit : α = .... ?

Momen gaya ialah bemasukan yang menyatakan besar gaya yang bekerja pada sebuah benda sehingga benda berotasi sedangkan momen inersia ialah sebuah bemasukan yang menyatakan kecenderungan benda untuk mempertahankan kedudukan biar tidak berotasi. Hubungan antara momen gaya dan momen inersia ditetapkan dengan persamaan diberikut:

τ = I .  α

F . d = I .  α

Keterangan :
τ = momen gaya atau torsi (Nm)
I = momen inersia benda ((kg m²)
F = gaya yang bekerja pada benda (N)
d = pajang lengan momen gaya (m)
α = percepatan tangensial.

Berdasarkan rumus di atas, maka diperoleh :
⇒ F . d  = I . α
⇒ F . R  = β . α
⇒ F . R = β. α
⇒ α = FR/β
⇒ α = F . R (β)^-1

Penyelesaian ringkas :
⇒ F . R = β. α
⇒ α = FR/β
⇒ α = F . R (β)^-1

Jadi, kekerabatan yang sempurna untuk menyatakan percepatan tangensial pada katrol tersebut ialah α = F . R (β)^-1.

Jawaban : D

Soal 3 : Menentukan Momen Gaya pada Batang

Sebuah batang yang sangat enteng, panjangnya 140 cm. Pada batang bekerja tiga gaya masing-masing F₁ = 20 N, F₂ = 10 N, dan F₃ = 40 N dengan arah dan posisi menyerupai pada gambar di bawah ini.

Besar momen gaya yang menjadikan batang berotasi pada sentra massanya ialah ....
A. 40 Nm
B. 39 Nm
C. 28 Nm
D. 14 Nm
E. 3 Nm

Pembahasan : 
Dik : L = 140 cm = 1,4 m, F₁ = 20 N, F₂ = 10 N, dan F₃ = 40 N
Dit : τ = .... ?

Jika pada suatu benda bekerja lebih dari satu gaya, maka momen gaya yang menjadikan benda tersebut berotasi ialah resultan dari masing-masing momen gaya yang bekerja pada benda tersebut. Pada soal ini disebutkan bahwa terdapat tiga gaya yang bekerja pada batang.

Momen gaya total yang dialami benda :

τ = ∑ F d  = F1.d1 +  F2.d2 + ..... Fn.dn

Keterangan :
τ = momen gaya yang bekerja pada benda (Nm)
F₁ = gaya pertama yang bekerja pada benda (Nm)
F₂ = gaya kedua yang bekerja pada benda (N)
d₁ = panjang lengan momen gaya pertama (m)
d₂ = pajang lengan momen gaya kedua (m).

Untuk menuntaskan soal menyerupai ini, maka yang harus diperhatikan ialah sumbu rotasi dan arah gaya yang bekerja. Pada soal ditanya momen gaya terhadap sentra massa. Pusat massa batang berada sempurna di tengah batang dan membagi batang mejadi dua belahan yang sama panjang. Perhatikan gambar diberikut ini.

Selanjutnya kita tinjau panjang lengan momen atau jarak masing-masing gaya ke sumbu rotasi (pusat massanya). Pada gambar di atas sudah diuraikan proses memilih panjang masing-masing lengan momen gaya. Sesudah itu perhatikan juga arah dari masing-masing gaya. Jumlahkan momen gaya yang searah dan kurangkan dengan momen gaya yang berlawanan arah.

Gaya F₁ dan F₃ sama-sama menghasilkan momen gaya yang memutar batang ke arah kiri (searah jarum jam) sedangkan gaya F₂ menghasilkan momen gaya yang memutar batang ke arah kanan (berlawanan arah jarum jam). melaluiataubersamaini demikian, momen gaya yang bekerja terhadap sentra massa:
⇒ τ = F₁.d₁ +  F₃.d₃ − F₂.d₂
⇒ τ = 20(140/2 cm) + 40(140/2 cm) − 10(70 cm - 40 cm)
⇒ τ = 20(70 cm) + 40(70 cm) − 10(30 cm)
⇒ τ = 20(0,7 m) + 40(0,7 m ) − 10(0,3 m)
⇒ τ = 14 + 28 - 3
⇒ τ = 39 Nm

Penyelesaian ringkas :
⇒ τ = F₁.d₁ +  F₃.d₃ − F₂.d₂
⇒ τ = 20(0,7) + 40(0,7) − 10(0,3)
⇒ τ = 14 + 28 - 3
⇒ τ = 39 Nm

Jadi, momen gaya yang menjadikan batang berotasi pada sentra massanya ialah 39 Nm.

Jawaban : B

Soal 4 : Menentukan Momen Gaya Terhadap Titik Tertentu

Sebuah batang yang diabaikan massanya dipengaruhi oleh tiga buah gaya yaitu F_A, F_B, dan F_C. Diketahui F_A = F_C = 10 N dan F_B = 20 N menyerupai pada gambar di bawah ini.

Jika jarak AB = BC = 20 cm, maka besar momen gaya terhadap titik C ialah ....
A. 0 Nm
B. 1 Nm
C. 4 Nm
D. 6 Nm
E. 8 Nm

Pembahasan :
Dik : F_A = F_C = 10 N, F_B = 20 N, d_AB = d_BC = 20 cm
Dit : τ = .... ?

Soal ini sanggup diselesaikan dengan konsep yang sama menyerupai soal nomor tiga. Yang harus diperhatikan ialah letak sumbu putarnya. Dalam soal ini sumbu rotasinya ialah titik C. Nah, sebab gaya C bekerja sempurna di titik C, maka momen gaya oleh gaya tersebut sama dengan nol sebab jaraknya sama dengan nol (τ = F . d = F . 0 = 0).

Karena momen gaya oleh F_C sama dengan nol, maka pada batang tersebut spesialuntuk ada dua gaya yang menghasilkan momen gaya, yaitu F_A dan F_B. Selanjutnya kita tinjau panjang lengan untuk kedua gaya tersebut. Berdasarkan gambar sanggup dilihat bahwa jarak A ke C ialah 40 cm sedangkan jarak B ke C ialah 20 cm.

Dari gambar juga sanggup dilihat bahwa gaya F_A dan F_B bekerja dalam arah yang berlawanan. melaluiataubersamaini demikian, momen gaya terhadap titik C adalah:
⇒ τ =  F_B.d_B − F_A.d_A
⇒ τ = 20(BC) − 10(AC)
⇒ τ = 20(20) − 10(40)
⇒ τ = 400 - 400
⇒ τ = 0

Penyelesaian ringkas :
⇒ τ =  F_B.d_BC − F_A.d_AC
⇒ τ = 20(20) − 10(40)
⇒ τ = 0

Jadi, momen gaya terhadap titik C ialah 0 Nm.

Jawaban : A

Soal 5 : Menentukan Momen Inersia Sistem

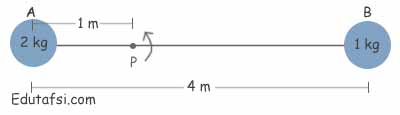
Tongkat penyambung tak bermassa sepanjang 4 m menghubungkan dua bola menyerupai terlihat pada gambar di bawah ini.

Momen inersia sistem jikalau diputar terhadap sumbu P yang berjarak 1 m di kanan bola A ialah ....
A. 5 kgm²
B. 7 kgm²
C. 9 kgm²
D. 10 kgm²
E. 11 kgm²

Pembahasan :
Dik : m_A = 2 kg, m_B = 1 kg, r_A = 1 m, r_B = 3 m
Dit : I = ..... ?

Momen inersia ialah bemasukan yang analog dengan massa untuk gerak rotasi. Jika massa mernyatakan tingkat kelembaman atau kecenderungan benda untuk mempertahankan posisinya, maka momen inersia ialah kecenderungan benda untuk mempertahankan posisi biar tidak berotasi.

Untuk sistem benda berupa partikel yang biasa dilukis berupa bulat kecil ataupun titik, momen inersia sistem sama dengan jumlah total dari momen inersia benda-benda yang ada dalam sistem tersebut. Secara matematis sanggup ditentukan dengan rumus diberikut ini:

I = ∑ m.r2 = m1.r12 + m2.r22 + ... + mn.rn2

Keterangan :
I = momen inersia sistem (kg m²)
m₁ = massa partikel pertama (kg)
r₁ = jarak partikel pertama ke sumbu rotasi (m)
m₂ = massa partikel kedua (kg)
r₂ = jarak partikel kedua ke sumbu rotasi (m).

Karena pada soal tidak disebutkan bolanya ialah bola pejal atau bola tipis berongga, maka kita asumsikan bola tersebut sebagai benda partikel. melaluiataubersamaini memakai rumus momen inersia sistem partikel, maka diperoleh :
⇒ I = ∑ m.r² 
⇒ I = m_A . r_A² + m_B . r_B²

Notasi r_A menyatakan jarak antara benda A ke sumbu rotasi (dalam soal sumbu rotasinya ialah titik P). Sedangkan notasi r_B menyatakan jarak antara benda B ke titik P. Karena jarak AB ialah 4 m dan jarak AP ialah 1 m, maka :
⇒ r_B = 4 - r_A
⇒ r_B = 4 - 1
⇒ r_B = 3 m

melaluiataubersamaini demikian, momen inersia sistem adalah:
⇒ I = 2(1)² + 1(3)²
⇒ I = 2 + 9
⇒ I = 11 kg m²

Penyelesaian ringkas :
⇒ I = m_A . r_A² + m_B . r_B²
⇒ I = 2(1)² + 1(3)²
⇒ I = 11 kg m²

Jadi, momen inersia sistem terhadap titik P ialah 11 kgm².

Jawaban : E

Demikian pembahasan soal ujian nasional bidang study fisika ihwal momen gaya dan momen inersia. Selain momen gaya, pada pembahasan selanjutnya juga ada soal UN Fisika ihwal katrol yang melibatkan momen inersia dan torsi. Jika pembahasan soal UN Fisika ini bermanfaa, menolong kami membagikannya kepada kawan-kawan anda melalui tombol share di bawah ini.