Pertidaksamaan linier dua variabel yaitu suatu pertidaksamaan yang memuat dua variabel dengan pangkat tertinggi satu.
Penyelesaian dari pertidaksamaa linier dua variabel ini ialah gambar tempat pada grafik Catesius (sumbu-XY) yang dibatasi oleh suatu garis linier
Untuk lebih jelasnya ikutilah teladan soal diberikut ini :
01. Tentukanlah tempat penyelesaian pertidaksamaan linier 2x + y ≤ 6, dengan x dan y anggota real.
Jawab
Pertama kita lukis garis 2x + y = 6 dengan menolongan tabel.
Selanjutnya diambil satu titik sembarang sebagai titik uji, contohnya O(0, 0), sehingga diperoleh 2(0) + 0 = 0 ≤ 6
Makara himpunan penyelesaiannya yakni tempat bab kiri bawah garis 2x + y = 6.
Jika beberapa pertidaksamaan linier bergabung dalam satu sistem, maka bentuk tersebut dinamakan sistem pertidaksamaan linier, dimana himpunan penyelesaiannya ialah irisan dari tempat penyelesaian masing-masing pertidaksamaan linier.
Untuk pemahaman lebih lanjut akan diuraikan pada teladan soal diberikut ini
02. Tentukanlah tempat penyelesaian dari sistem pertidaksamaan linier :
2x + 3y ≤ 12 , x ≥ 1 , y ≥ 1
Jawab
Pertama akan dilukis garis 2x + 3y = 6, garis x= 1 dan garis y = 1 ke dalam satu tatanan koordinat Cartesius
Himpunan penyelesaiannya yakni tempat segitiga yang bebas dari arsiran
02. Tentukanlah tempat penyelesaian dari sistem pertidaksamaan linier ;
2x + y ≤ 8 , 4x + 5y ≤ 20 , x ≥ 0 , y ≥ 0
Jawab
Pertama akan dilukis garis 2x + y = 8 dan garis 4x + 5y = 20 ke dalam satu tatanan koordinat Cartesius
Himpunan penyelesaiannya yakni tempat segiempat yang bebas dari arsiran
03. Tentukanlah sistem pertidaksamaan untuk dearah yang diarsir pada gambar di bawah ini.
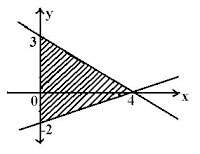
04. Tentukanlah sistem pertidaksamaan untuk dearah yang diarsir pada gambar di bawah ini.
Jawab
Persamaan garis yang melalui titik (4,0) dan (0, 3) adalah
Persamaan garis yang melalui titik (4,0) dan (0, -2) adalah
Sehingga sistem pertidaksamaan linier untuk gambar di atas yakni :
3x + 4y ≤ 12
x – 2y ≤ 4
x ≥ 0
Dalam kehidupan sehari-hari, aneka macam masalah-masalah yang penyelesaiannya memakai sistem pertidaksamaan linier ini. Proses menuntaskan problem sehari-hari dengan memakai sistem pertidaksamaan linier ini dinamakan Program Linier. Tentu saja, tahap awal proses ini yakni mengubah informasi informasi dalam soal dongeng menjadi suatu sistem pertidaksamaan linier. Tahap ini dinamakan tahap menyusun model matemetika. Sesudah itu digambar tempat penyelesaian dari sistem pertidaksamaan linier yang sudah diperoleh.
Untuk lebih jelasnya ikutilah teladan soal diberikut ini.
05. Suatu jenis makanan ternak membutuhkan 5 kg daging dan 3 kg tepung. Makanan ternak jenis lain membutuhkan 6 kg daging dan 8 kg tepung. Jika tersedia daging 60 kg dan tepung 48 kg, sedangkan materi yang lain cukup tersedia, maka Gambarlah tempat penyelesaian sistem pertidaksamaan liniernya.
Jawab
Misalkan
x = banyaknya makanan ternak jenis pertama
y = banyaknya makanan ternak jenis kedua
maka model matemaikanya sanggup ditentukan dengan menolongan tabel
Dari tabel di atas sanggup disusun sistem pertidaksamaan liniernya, yakni :
5x + 6y ≤ 60
3x + 8y ≤ 48
x ≥ 0
y ≥ 0
Selanjutnya digambar tempat penyelesaiannya ke dalam koordinat Cartesius
Himpunan penyelesaiannya yakni tempat segiempat yang bebas dari arsiran.
09. Seorang pedagang mainan ingin membeli mainan untuk persediaan di tokonya maksimum 100 paket. Mainan yang akan dibeli yakni jenis A dengan harga Rp 6.000 perpaket dan jenis B seharga Rp. 8.000 perpaket. Uang yang tersedia untuk modal yakni Rp. 720.000. Gambarlah tempat penyelesaian sistem pertidaksamaan liniernya biar manfaatnya makasimum
Jawab
Misalkan x = banyaknya mainan jenis A
y = banyaknya mainan jenis B
maka sistem pertidaksamaannya sanggup ditentukan sebagai diberikut :
x + y ≤ 100 .................................... x + y ≤ 100
6000x + 8000y ≤ 720000 ...............3x + 4y ≤ 360
x ≥ 0
y ≥ 0
Selanjutnya digambar tempat penyelesaiannya ke dalam koordinat Cartesius
Penyelesaian dari pertidaksamaa linier dua variabel ini ialah gambar tempat pada grafik Catesius (sumbu-XY) yang dibatasi oleh suatu garis linier
Untuk lebih jelasnya ikutilah teladan soal diberikut ini :
01. Tentukanlah tempat penyelesaian pertidaksamaan linier 2x + y ≤ 6, dengan x dan y anggota real.
Jawab
Pertama kita lukis garis 2x + y = 6 dengan menolongan tabel.
Selanjutnya diambil satu titik sembarang sebagai titik uji, contohnya O(0, 0), sehingga diperoleh 2(0) + 0 = 0 ≤ 6
Makara himpunan penyelesaiannya yakni tempat bab kiri bawah garis 2x + y = 6.
Jika beberapa pertidaksamaan linier bergabung dalam satu sistem, maka bentuk tersebut dinamakan sistem pertidaksamaan linier, dimana himpunan penyelesaiannya ialah irisan dari tempat penyelesaian masing-masing pertidaksamaan linier.
Untuk pemahaman lebih lanjut akan diuraikan pada teladan soal diberikut ini
02. Tentukanlah tempat penyelesaian dari sistem pertidaksamaan linier :
2x + 3y ≤ 12 , x ≥ 1 , y ≥ 1
Jawab
Pertama akan dilukis garis 2x + 3y = 6, garis x= 1 dan garis y = 1 ke dalam satu tatanan koordinat Cartesius
Himpunan penyelesaiannya yakni tempat segitiga yang bebas dari arsiran
02. Tentukanlah tempat penyelesaian dari sistem pertidaksamaan linier ;
2x + y ≤ 8 , 4x + 5y ≤ 20 , x ≥ 0 , y ≥ 0
Jawab
Pertama akan dilukis garis 2x + y = 8 dan garis 4x + 5y = 20 ke dalam satu tatanan koordinat Cartesius
Himpunan penyelesaiannya yakni tempat segiempat yang bebas dari arsiran
03. Tentukanlah sistem pertidaksamaan untuk dearah yang diarsir pada gambar di bawah ini.
Untuk memilih sistem pertidaksamaan pada gambar di atas, harus ditentukan terlebih lampau persamaan garis lurus yang menjadi batas-batas daerahnya, yakni dengan memakai rumus :
Sehingga sistem pertidaksamaan linier untuk gambar di atas yakni :
3x + 2y ≤ 12
x + 2y ≤ 8
x ≥ 0
y ≥ 0
Catatan : Jika kedua titik yang terletak pada garis lurus tersebut, diketahui berada pada sumbu-X dan sumbu-Y,
04. Tentukanlah sistem pertidaksamaan untuk dearah yang diarsir pada gambar di bawah ini.
Jawab
Persamaan garis yang melalui titik (4,0) dan (0, 3) adalah
Persamaan garis yang melalui titik (4,0) dan (0, -2) adalah
Sehingga sistem pertidaksamaan linier untuk gambar di atas yakni :
3x + 4y ≤ 12
x – 2y ≤ 4
x ≥ 0
Dalam kehidupan sehari-hari, aneka macam masalah-masalah yang penyelesaiannya memakai sistem pertidaksamaan linier ini. Proses menuntaskan problem sehari-hari dengan memakai sistem pertidaksamaan linier ini dinamakan Program Linier. Tentu saja, tahap awal proses ini yakni mengubah informasi informasi dalam soal dongeng menjadi suatu sistem pertidaksamaan linier. Tahap ini dinamakan tahap menyusun model matemetika. Sesudah itu digambar tempat penyelesaian dari sistem pertidaksamaan linier yang sudah diperoleh.
Untuk lebih jelasnya ikutilah teladan soal diberikut ini.
05. Suatu jenis makanan ternak membutuhkan 5 kg daging dan 3 kg tepung. Makanan ternak jenis lain membutuhkan 6 kg daging dan 8 kg tepung. Jika tersedia daging 60 kg dan tepung 48 kg, sedangkan materi yang lain cukup tersedia, maka Gambarlah tempat penyelesaian sistem pertidaksamaan liniernya.
Jawab
Misalkan
x = banyaknya makanan ternak jenis pertama
y = banyaknya makanan ternak jenis kedua
maka model matemaikanya sanggup ditentukan dengan menolongan tabel
Dari tabel di atas sanggup disusun sistem pertidaksamaan liniernya, yakni :
5x + 6y ≤ 60
3x + 8y ≤ 48
x ≥ 0
y ≥ 0
Selanjutnya digambar tempat penyelesaiannya ke dalam koordinat Cartesius
Himpunan penyelesaiannya yakni tempat segiempat yang bebas dari arsiran.
09. Seorang pedagang mainan ingin membeli mainan untuk persediaan di tokonya maksimum 100 paket. Mainan yang akan dibeli yakni jenis A dengan harga Rp 6.000 perpaket dan jenis B seharga Rp. 8.000 perpaket. Uang yang tersedia untuk modal yakni Rp. 720.000. Gambarlah tempat penyelesaian sistem pertidaksamaan liniernya biar manfaatnya makasimum
Jawab
Misalkan x = banyaknya mainan jenis A
y = banyaknya mainan jenis B
maka sistem pertidaksamaannya sanggup ditentukan sebagai diberikut :
x + y ≤ 100 .................................... x + y ≤ 100
6000x + 8000y ≤ 720000 ...............3x + 4y ≤ 360
x ≥ 0
y ≥ 0
Selanjutnya digambar tempat penyelesaiannya ke dalam koordinat Cartesius


















Emoticon