Pembahasan Soal Un Dimensi Tiga

Pembahasan soal Ujian Nasional (UN) Matematika IPA jenjang pendidikan Sekolah Menengan Atas untuk pokok bahasan Dimensi Tiga yang mencakup jarak atau sudut antara titik, garis dan bidang.

Berikut beberapa konsep yang dipakai pada pembahasan :

1. UN 2008
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Jarak titik H ke garis AC yaitu ...
A.  8√3
B.  8√2
C.  4√6
D.  4√3
E.  4√2

Pembahasan :

Jarak titik H ke garis AC yaitu OH.
rusuk = a = 8
OH = \(\mathrm{\frac{a}{2}}\)√6 = \(\frac{8}{2}\)√6 = 4√6

Jawaban : C


2. UN 2010
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Titik P yaitu titik potong AH dan ED dan titik Q yaitu titik potong FH dan EG. Jarak titik B ke garis PQ yaitu ...
A.  √22  cm
B.  √21  cm
C.  2√5  cm
D.  √19  cm
E.  3√2  cm

Pembahasan :

Jarak titik B ke garis PQ yaitu BR.
rusuk = a = 4

BP = BQ = \(\mathrm{\frac{a}{2}}\)√6 = \(\frac{4}{2}\)√6 = 2√6
PQ = \(\mathrm{\sqrt{PS^{2}+SQ^{2}}=\sqrt{2^{2}+2^{2}}=2\sqrt{2}}\)

BPQ sama kaki sehingga :
PR = RQ = \(\frac{1}{2}\)PQ = \(\frac{1}{2}\)(2√2) = √2

Perhatikan segitiga BPR siku-siku di R
BR = \(\mathrm{\sqrt{BP^{2}-PR^{2}}}\)
BR = \(\mathrm{\sqrt{\left (2\sqrt{6}  \right )^{2}-\left ( \sqrt{2} \right )^{2}}}\)
BR = \(\mathrm{\sqrt{22}}\)

Jawaban : A


3. UN 2011
Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. M yaitu titik tengah EH. Jarak titik M ke AG yaitu ...
A.  4√6  cm
B.  4√5  cm
C.  4√3  cm
D.  4√2  cm
E.  4  cm

Pembahasan :

Jarak titik M ke garis AG yaitu MO
a = 8

Perhatikan bahwa garis MN dan AG berpotongan tegak lurus dan sama besar di titik O, sehingga
MO = \(\frac{1}{2}\). MN
MO = \(\frac{1}{2}\). a√2
MO = \(\frac{1}{2}\). 8√2
MO = 4√2

Jawaban : D


4.  UN 2007
Diketahui kubus ABCD.EFGH dengan rusuk 6√3 cm. Jarak Bidang ACH dan EGB yaitu ...
A.  4√3  cm
B.  2√3  cm
C.  4  cm
D.  6  cm
E.  12  cm

Pembahasan :

Jarak bidang ACH dan EGB = jarak garis OH dan BR = jarak titik P dan Q  ⇒ PQ.

rusuk = a = 6√3
OH = BR = \(\mathrm{\frac{a}{2}}\)√6 = 9√2
OR = a = 6√3
HF = a√2 = 6√6
HR = \(\frac{1}{2}\) × HF = 3√6
DF = a√3 = 18

Perhatikan bidang BDHF

OHRB yaitu jajar genjang dengan bantalan OH dan tinggi PQ
Ingat : luas jajar genjang \(\mathrm{=alas\times tinggi}\)

Luas jajar genjang OHRB = 2 × luas ⊿ OHR
OH × PQ = 2 × \(\frac{1}{2}\)×HR×OR
OH × PQ = HR × OR
9√2 × PQ = 3√6 × 6√3
⇒ PQ = 6

atau
DP = PQ = QF = \(\frac{1}{3}\) × DF
DP = PQ = QF = \(\frac{1}{3}\) × 18
⇒ PQ = 6

Jawaban : D


5. UN 2009
Diketahui kubus ABCD.EFGH, panjang rusuk kubus yaitu 12 cm. Titik P terletak pada perpantidakboleh rusuk DC sehingga CP : DP = 1 : 3. Jarak titik P dengan bidang BDHF yaitu ...
A.  6√2  cm
B.  9√2  cm
C.  12√2  cm
D.  16√2  cm
E.  18√2  cm

Pembahasan :

Jarak titik P ke bidang BDHF = jarak titik P ke garis BD  ⇒ PQ.
rusuk = a = 12
CP : DP = 1 : 3  ⇒  DC : CP = 2 : 1
DC = 12  ⇒ CP = 6
DP = DC + CP = 12 + 6 =18
BD = a√2 = 12√2

Perhatikan segitiga BDP

melaluiataubersamaini memakai rumus luas segitiga diperoleh :
\(\frac{1}{2}\) × BD × PQ = \(\frac{1}{2}\) × DP × BC
 BD × PQ = DP × BC
12√2 × PQ = 18 × 12
⇒ PQ = 9√2

Jawaban : B


6. UN 2012
Kubus ABCD.EFGH dengan rusuk 4 cm. Jarak titik H ke bidang ACF yaitu ...
A.  \(\frac{2}{3}\)√3  cm
B.  \(\frac{4}{3}\)√3  cm
C.  \(\frac{11}{3}\)√3  cm
D.  \(\frac{8}{3}\)√3  cm
E.  \(\frac{13}{3}\)√3  cm

Pembahasan :

Jarak titik H ke bidang ACF = jarak titik H ke garis OF = jarak titik H ke titik P  ⇒ HP.
rusuk = a = 4
OF = OH = \(\mathrm{\frac{a}{2}}\)√6 = 2√6
FH = a√2 = 4√2
OQ = a = 4

Perhatikan segitiga OFH

HP dan OQ ialah garis tinggi, sehingga dengan memakai rumus luas segitiga akan diperoleh persamaan sebagai diberikut ;
\(\frac{1}{2}\)×OF×HP = \(\frac{1}{2}\)×FH×OQ
OF × HP = FH × OQ
2√6 × HP = 4√2 × 4
⇒ HP = \(\mathrm{\frac{8}{3}}\)√3

HP = \(\mathrm{\frac{2}{3}}\) × HB
HP = \(\mathrm{\frac{2}{3}}\) × a√3
HP = \(\mathrm{\frac{2}{3}}\) × 4√3
HP = \(\mathrm{\frac{8}{3}}\)√3

Jawaban : D


7. UN 2013
Kubus ABCD.EFGH mempunyai panjang rusuk 6 cm. Jarak titik B ke CE yaitu ...
A.  \(\frac{1}{2}\)√3  cm
B.  \(\frac{1}{2}\)√6  cm
C.  3√3  cm
D.  2√6  cm
E.  4√6  cm

Pembahasan :

Jarak B ke CE yaitu BP
a = 6
BC = a = 6
BE = a√2 = 6√2
CE = a√3 = 6√3

Perhatikan Δ BCE siku-siku di B

BP = \(\mathrm{\frac{BC\times BE}{CE}}\)
BP = \(\mathrm{\frac{6\times 6\sqrt{2}}{6\sqrt{3}}}\)
BP = 2√6

Jawaban : D


8. UN 2014
Diketahui limas beraturan T.ABCD dengan ABCD yaitu persegi yang mempunyai panjang AB = 4 dan TA = 6 cm. Jarak titik C ke garis AT = ...
A.  \(\frac{1}{14}\)√14  cm
B.  \(\frac{2}{3}\)√14  cm
C.  \(\frac{3}{4}\)√14  cm
D.  \(\frac{4}{3}\)√14  cm
E.  \(\frac{3}{2}\)√14  cm

Pembahasan :

Jarak C ke AT yaitu CP
AT = CT = 6
AC = 4√2

Perhatikan  Δ ACT

AP = \(\mathrm{\frac{AT^{2}+AC^{2}-CT^{2}}{2\times AT}}\)
AP = \(\mathrm{\frac{6^{2}+\left ( 4\sqrt{2} \right )^{2}-6^{2}}{2\times 6}}\)
AP = \(\mathrm{\frac{8}{3}}\)

Perhatikan Δ APC siku-siku di P
CP = \(\mathrm{\sqrt{AC^{2}-AP^{2}}}\)
CP = \(\mathrm{\sqrt{\left ( 4\sqrt{2} \right )^{2}-\left ( \frac{8}{3} \right )^{2}}}\)
CP = \(\mathrm{\frac{4}{3}\sqrt{14}}\)

Jawaban : D


9. UN 2004
Panjang rusuk kubus ABCD.EFGH yaitu 6 cm. Jika S yaitu titik potong EG dan FH, maka jarak DH ke AS yaitu ... cm.
A.  2√3
B.  4
C.  3√2
D.  2√6
E.  6

Pembahasan :

Jarak DH ke AS yaitu HS, sebab HS tegak lurus terhadap DH dan AS.
rusuk = a = 6
HF = a√2 = 6√2
HS = \(\frac{1}{2}\). HF
HS = \(\frac{1}{2}\). 6√2
HS = 3√2

Jawaban : C


10. UN 2007
Diketahui sebuah kubus ABCD. EFGH. Besar sudut yang dibuat oleh garis BG dengan BDHF yaitu ...
A.  90°
B.  60°
C.  45°
D.  30°
E.  15°

Pembahasan :

Misalkan sudut yang dibuat oleh BG dengan BDHF yaitu β.
rusuk = a
BG = EG = a√2
PG = \(\frac{1}{2}\) × EG = \(\mathrm{\frac{a}{2}}\)√2

Perhatikan Δ BPG siku-siku di P
sin β = \(\mathrm{\frac{PG}{BG}}\) = \(\mathrm{\frac{\frac{a}{2}\sqrt{2}}{a\sqrt{2}}}\) = \(\frac{1}{2}\)

Karena sin β = \(\frac{1}{2}\), maka β = 30°

Jawaban : D


11. UN 2008
Diketahui kubus dengan panjang rusuk 6 cm. Jika sudut antara diagonal AG dengan bidang bantalan ABCD yaitu α, maka sin α yaitu ...
A. \(\frac{1}{2}\)√3
B. \(\frac{1}{2}\)√2
C. \(\frac{1}{3}\)√3
D. \(\frac{1}{2}\)E. \(\frac{1}{3}\)√2

Pembahasan :



Sudut antara AG dengan bidang bantalan ABCD yaitu α.
rusuk = a = 6
CG = a = 6
AG = a√3 = 6√3

Perhatikan Δ ACG siku-siku di C
sin α = \(\mathrm{\frac{CG}{AG}}\) = \(\mathrm{\frac{6}{6\sqrt{3}}}\) = \(\frac{1}{3}\)√3

Jawaban : C


12. UN 2009
Balok ABCD. EFGH dengan panjang AB = BC = 3 cm dan AE = 5 cm. P terletak pada AD sehingga AP : PD = 1 : 2 dan Q terletak pada EG sehingga FQ : QG = 2 : 1. Jika α yaitu sudut antara PQ dengan ABCD, maka tan α yaitu ...
A. \(\frac{1}{2}\)√5
B. \(\frac{1}{10}\)√10
C. \(\frac{1}{2}\)√10
D. \(\frac{1}{7}\)√14
E. \(\frac{1}{7}\)√35

Pembahasan :



Sudut antara PQ dengan ABCD yaitu α.
QR = 5
PS = 3
BS = SR = RC = 1
PR = \(\mathrm{\sqrt{PS^{2}+SR^{2}}=\sqrt{3^{2}+1^{2}}}\)
PR = \(\mathrm{\sqrt{10}}\)

Perhatikan Δ PQR siku-siku di R
tan α = \(\mathrm{\frac{QR}{PR}}\) = \(\mathrm{\frac{5}{\sqrt{10}}}\) = \(\frac{1}{2}\sqrt{10}\)

Jawaban : C


13. UN 2012
Diketahui limas segi empat beraturan P.QRST, dengan rusuk bantalan 3 cm dan rusuk tegak 3√2 cm. Tangan sudut antara garis PT dan bantalan QRST yaitu ...
A. \(\frac{1}{3}\)√3
B. √2
C. √3
D. 2√2
E. 2√3

Pembahasan :



Misalkan sudut antara garis PT dan bantalan QRST yaitu θ.
QR = RS = ST = QT = 3
PQ = PR = PS = PT = 3√2
RT = a√2 = 3√2

Perhatikan bahwa PRT yaitu segitiga sama sisi karena
PR = RT = PT = 3√2
sehingga θ = 60°
tan θ = tan 60° = √3

Jawaban : C


14. UN 2013
Pada kubus ABCD. EFGH sudut θ yaitu sudut antara bidang BDE dengan bidang ABCD. Nilai dari sin θ yaitu ...
A. \(\frac{1}{4}\)√3
B. \(\frac{1}{2}\)√3
C. \(\frac{1}{3}\)√6
D. \(\frac{1}{2}\)√2
E. \(\frac{1}{3}\)√3

Pembahasan :



Sudut antara bidang BDE dengan bidang ABCD yaitu θ.
misalkan rusuk = a
AE = a
EO = \(\mathrm{\frac{a}{2}}\)√6

Perhatikan Δ AOE siku-siku di A
sin θ = \(\mathrm{\frac{AE}{EO}}\) =\(\mathrm{\frac{a}{\frac{a}{2}\sqrt{6}}}\) = \(\frac{2}{\sqrt{6}}\) = \(\frac{1}{3}\)√6

Jawaban : C


15. UN 2014
Kubus ABCD.EFGH mempunyai rusuk 4 cm. Sudut antara AE dan bidang AFH yaitu α. Nilai sin α yaitu ...
A. \(\frac{1}{2}\)√2
B. \(\frac{1}{2}\)√3
C. \(\frac{1}{3}\)√3
D. \(\frac{2}{3}\)√2
E. \(\frac{3}{4}\)√3

Pembahasan :



Sudut antara AE dan bidang AFH yaitu α
rusuk = a = 4
EG = a√2 = 4√2
EO = \(\mathrm{\frac{1}{2}}\) × EG = 2√2
AO = \(\mathrm{\frac{a}{2}}\)√6 = 2√6

Perhatikan Δ AEO siku-siku di E
sin α = \(\mathrm{\frac{EO}{AO}}\) = \(\mathrm{\frac{2\sqrt{2}}{2\sqrt{6}}=\frac{\sqrt{2}}{\sqrt{6}}}\) = \(\frac{1}{3}\)√3

Jawaban : C


16. UN 2007
Diketahui bidang 4 beraturan ABCD dengan panjang rusuk 8 cm. Kosinus sudut antara bidang ABC dan bidang ABD yaitu ...
A. \(\frac{1}{3}\)

B. \(\frac{1}{2}\)
C. \(\frac{1}{3}\)√3
D. \(\frac{2}{3}\)
E. \(\frac{1}{2}\)√3

Pembahasan :



Misalkan sudut antara bidang ABC dan ABD yaitu θ.

Karena berdiri diatas ialah bidang empat beraturan, pastilah ke-4 bidangnya ialah segitiga sama sisi.
rusuk (a) = 8
DC = a = 8
PC = PD = \(\mathrm{\frac{a}{2}}\)√3 = 4√3

Perhatikan Δ PCD, dengan hukum cosinus diperoleh :
cos θ = \(\mathrm{\frac{PC^{2}+PD^{2}-DC^{2}}{2\times PC\times PD}}\)
cos θ = \(\mathrm{\frac{\left ( 4\sqrt{3} \right )^{2}+\left ( 4\sqrt{3} \right )^{2}-8^{2}}{2\times 4\sqrt{3}\times 4\sqrt{3}}}\)
cos θ = \(\frac{1}{3}\)

Jawaban : A


17. UN 2015
Kubus ABCD. EFGH dengan rusuk 12 cm, tangen sudut antara bidang AFH dengan bidang CFH adalah...
A. \(\frac{1}{3}\)
B. \(\frac{1}{2}\)√2
C. \(\frac{2}{3}\)√2
D. √2
E. 2√2

Pembahasan :



Misalkan sudut antara bidang AFH dan CFH yaitu θ.

Perhatikan segitiga ACP
AP = CP = \(\mathrm{\frac{a}{2}}\)√6 = \(\frac{12}{2}\)√6 = 6√6
AC = a√2 = 12√2

melaluiataubersamaini hukum cosinus
Cos θ = \(\mathrm{\frac{AP^{2}+CP^{2}-AC^{2}}{2\,.\,AP\,.\,CP}}\)
Cos θ = \(\mathrm{\frac{(6\sqrt{6})^{2}+(6\sqrt{6})^{2}-(12\sqrt{2})^{2}}{2\,.\,6\sqrt{6}\,.\,6\sqrt{6}}}\)
Cos θ = \(\frac{216+216-288}{432}\)
Cos θ = \(\frac{1}{3}\)

Cos θ = \(\frac{1}{3}\)
sisi samping = 1
sisi miring = 3
sisi depan = \(\sqrt{3^{2}-1^{2}}\) = √8 = 2√2
tan θ = \(\mathrm{\frac{depan}{samping}}\) = \(\frac{2\sqrt{2}}{1}\) = 2√2

Jadi, tangen sudut antara bidang AFH dan CFH yaitu 2√2.

Jawaban : E

18. UN 2015
Diketahui kubus ABCD. EFGH dengan panjang rusuk 4 cm. Titik M yaitu titik tengah AB. Jarak titik E ke CM sama dengan...
A. \(\frac{4}{5}\)√30 cm
B. \(\frac{2}{3}\)√30 cm
C. 2√5 cm
D. 2√3 cm
E. 2√2 cm

Pembahasan :



CM = EM = \(\mathrm{\frac{a}{2}}\)√5 = \(\frac{4}{2}\)√5 = 2√5
CE = a√3 = 4√3
MN = a√2 = 4√2
Karena MN dan CE berpotongan tegak lurus dan sama besar di titik Q, maka
MQ = \(\frac{1}{2}\)×MN = 2√2

Perhatikan segitiga CEM, ∠M yaitu sudut tumpul sebab CE2 > CM2 + EM2, sehingga jarak titik E ke CM yaitu jarak dari titik E ke perpantidakboleh CM yaitu EP.

melaluiataubersamaini memakai rumus luas segitiga pada segitiga CEM akan diperoleh persamaan sebagai diberikut :
\(\frac{1}{2}\)×CM×EP = \(\frac{1}{2}\)×CE×MQ
CM × EP = CE × MQ
2√5 × EP = 4√3 × 2√2 (kali √5)
10 × EP = 8√30
EP = \(\frac{4}{5}\)√30

Jawaban : A


RALAT : 10/8/2017
Yang ditanyakan yaitu jarak titik E ke CM, bukan jarak titik E ke perpantidakboleh CM.
CM yaitu ruas garis, dengan titik-titik ujungnya C dan M. Jadi, jarak titik E ke CM yaitu jarak terdekat dari titik E ke ruas garis CM, yaitu EM = 2√5 (C)

19. UN 2016
Diketahui kubus ABCD EFGH dengan panjang rusuk 8 cm. Jarak titik E ke garis FD adalah...
A. \(\frac{8}{3}\)√2 cm
B. \(\frac{8}{3}\)√3 cm
C. \(\frac{8}{3}\)√6 cm
D. \(\frac{10}{3}\)√6 cm
E. 4√6 cm

Pembahasan :



Jarak titik E ke garis FD yaitu EP.

Perhatikan segitiga DEF siku-siku di E
EF = 8
DE = 8√2
DF = 8√3



EP = \(\mathrm{\frac{DE \times EF}{DF}}\)
EP = \(\mathrm{\frac{8\sqrt{2} \times 8}{8\sqrt{3}}}\)
EP = \(\frac{8}{3}\)√6

Jawaban : C


20. UN 2016
Diketahui kubus ABCD EFGH dengan AB = 16 cm. Nilai sinus sudut antara garis AH dengan bidang BDHF adalah...
A. \(\frac{1}{2}\)
B. \(\frac{1}{3}\)√3
C. \(\frac{1}{2}\)√2
D. \(\frac{1}{2}\)√3
E. \(\frac{1}{3}\)√6

Pembahasan :



Misalkan sudut yang dibuat oleh AH dengan BDHF yaitu θ.
rusuk = a = 16 cm
AH = AC = a√2 = 16√2
AP = \(\frac{1}{2}\)×AC = 8√2

Perhatikan Δ AHP siku-siku di P
sin θ = \(\mathrm{\frac{AP}{AH}}\) = \(\mathrm{\frac{8\sqrt{2}}{16\sqrt{2}}}\) = \(\frac{1}{2}\)

Jawaban : A

UPDATE 21/10/17

Untuk Ujian Nasional matematika IPA tahun 2017, bahan dimensi tiga dikeluarkan sebanyak 4 soal dalam satu paket.

21. UN 2017
Diketahui kubus ABCD.EFGH dengan panjang rusuknya 6 cm. Jika α yaitu sudut antara bidang AFH dan bidang BDHF, nilai sin α = ...
A.  1/2
B.  1/3 √3
C.  1/2 √2
D.  1/2 √3
E.  2/3 √2

Pembahasan :

AC = a√2 = 6√2
AP =  \(\frac{1}{2}\). AC = 3√2
AO = \(\mathrm{\frac{a}{2}}\)√6 = 3√6

Perhatikan segitiga AOP siku-siku di P.
sin α = \(\mathrm{\frac{AP}{AO}}\) = \(\frac{3\sqrt{2}}{3\sqrt{6}}\) = \(\frac{1}{3}\)√3

Jawaban : B


22. UN 2017
Diketahui kubus KLMN.OPQR dengan panjang rusuknya 6 cm. Jarak titik M ke bidang LNQ yaitu ...
A.  2√2  cm
B.  2√3  cm
C.  3√2  cm
D.  3√3  cm
E.  4√3  cm

Pembahasan :
Jarak M ke LNQ = jarak M ke QS, yaitu MT.

SM = \(\frac{1}{2}\). KM = 3√2
MQ = 6
SQ = \(\mathrm{\frac{a}{2}}\)√6 = 3√6

Perhatikan segitiga SMQ siku-siku di M. Pada segitiga siku-siku, jarak dari titik sudut siku-siku ke sisi miringnya yaitu hasil kali dari kedua sisi siku-siku dibagi sisi miring.
Jadi, MT = \(\mathrm{\frac{SM \,\cdot \,MQ}{SQ}}\) = \(\mathrm{\frac{6\, \cdot \,3\sqrt{2}}{3\sqrt{6}}}\) = 2√3

atau

MT = \(\frac{1}{3}\). MO = \(\frac{1}{3}\). 6√3 = 2√3

Jawaban : B


23. UN 2017
Diketahui limas beraturan T.ABCD. Panjang rusuk tegak dan panjang rusuk bantalan 4 cm. Jarak titik A ke TB yaitu ...
A.  2√2  cm
B.  2√3  cm
C.  4  cm
D.  4√2  cm
E.  4√3  cm

Pembahasan :
Jadi, jarak titik A ke TB yaitu AP.

Perhatikan segitiga sama sisi ABT dengan panjang sisinya 4 cm. Pada segitiga sama sisi yang panjang sisinya a, jarak dari titik sudut ke sisi di depannya yaitu \(\mathrm{\frac{a}{2}}\)√3.

Jadi, jarak titik A ke TB adalah
AP = \(\mathrm{\frac{4}{2}}\)√3 = 2√3

Jawaban : B



24. UN 2017
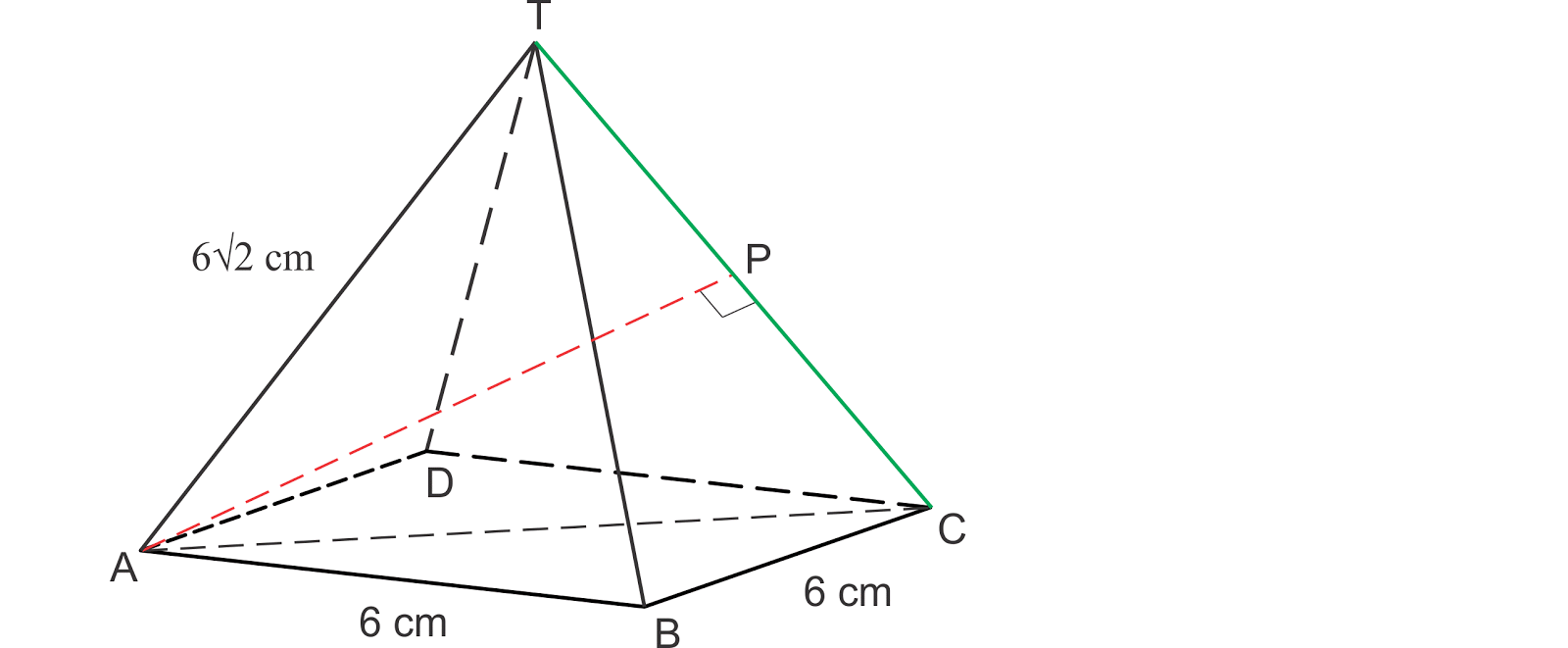
Diketahui limas beraturan T.ABCD dengan panjang rusuk tegak 6√2 cm dan panjang rusuk bantalan 6 cm. Jarak titik A ke TC yaitu ...
A.  2√2  cm
B.  2√3  cm
C.  3√2  cm
D.  3√3  cm
E.  3√6  cm

Pembahasan :
Jarak titik A ke TC yaitu AP.

AC = a√2 = 6√2
Karena AC = TC = AT, maka ACT yaitu segitiga sama sisi dengan panjang sisi 6√2.

Jadi, AP = \(\mathrm{\frac{6\sqrt{2}}{2}}\)√3 = 3√6

Jawaban : E


25. UN 2017
Diketahui limas bantalan segiempat beraturan T.ABCD. Panjang rusuk tegak = rusuk bantalan = 4 cm. Sudut antara garis TA dan bidang bantalan ABCD yaitu ...
A.  15°
B.  30°
C.  45°
D.  60°
E.  90°

Pembahasan :
Misalkan sudut antara garis TA dan bidang bantalan ABCD yaitu α.

AC = 4√2
AO = \(\frac{1}{2}\). AC = 2√2
AT = 4

Perhatikan segitiga AOT siku-siku di O.
cos α = \(\mathrm{\frac{AO}{AT}}\) = \(\frac{2\sqrt{2}}{4}\) = \(\frac{1}{2}\)√2
Karena cos α = \(\frac{1}{2}\)√2 maka α = 45°

Jawaban : C


26. UN 2017
Diketahui limas segienam beraturan T.ABCDEF rusuk alasnya 6 cm dan tinggi limas 6√3 cm. Nilai sinus sudut antara rusuk tegak dan bidang bantalan limas yaitu ...
A.  1/3 √2
B.  1/2
C.  1/3 √3
D.  1/2 √2
E.  1/2 √3

Pembahasan :
Misalkan sudut antara rusuk tegak dengan bidang bantalan yaitu α.

Perhatikan segitiga COT siku-siku di O.
CT = \(\mathrm{\sqrt{\left (CO  \right )^{2}+\left (OT  \right )^{2}}}\)
CT = \(\mathrm{\sqrt{\left (6  \right )^{2}+\left (6\sqrt{3}  \right )^{2}}}\)
CT = 12

sin α = \(\mathrm{\frac{OT}{CT}}\) = \(\frac{6\sqrt{3}}{12}\) = \(\frac{1}{2}\)√3

atau

tan α = \(\mathrm{\frac{OT}{CO}}\) = \(\frac{6\sqrt{3}}{6}\) = √3
Karena tan α = √3, maka α = 60°
Jadi, sin α = sin 60° = \(\frac{1}{2}\)√3

Jawaban : E


27. UN 2017
Diketahui kubus ABCD.EFGH, panjang rusuknya 12 cm dan α yaitu sudut antara bidang BDG dan ABCD. Nila sin α yaitu ...
A.  1/6 √6
B.  1/3 √3
C.  1/2 √2
D.  1/3 √6
E.  1/2 √3

Pembahasan :

CG = a = 12
OG = \(\mathrm{\frac{a}{2}}\)√6 = 6√6

Perhatikan segitiga OCG siku-siku di C.
sin α = \(\mathrm{\frac{CG}{OG}}\) = \(\frac{12}{6\sqrt{6}}\) = \(\frac{1}{3}\)√6

Jawaban : D